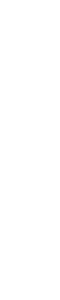Quantum Advantage – Are We There Yet? (Part 2)

This is the second in a three-part series exploring the quantum advantage that purports to accelerate drug discoveries, render current cryptographic techniques obsolete, turbocharge AI and machine learning, and basically solve the world’s problems. This part will explore properties of quantum mechanics to provide an understanding of the principles underlying quantum computers and their operations.
Quantum basics
Quantum mechanics is the field of study of the very small things – and by very small, I mean atoms and the particles that make up atoms. Quantum mechanics concerns the behaviour and interaction of matter at an atomic and subatomic scale.
Particle-wave duality
We can ease into quantum science by looking at how light behaves. Light behaves in some aspects as a particle, and in other aspects like a wave. The double slit experiment illustrates this.
Imagine having a paintball gun. You shoot paintballs at a wall that has two slits, and behind the wall with slits is a second wall. Some of the splats will hit the first wall, and some will go through one or the other of the slits. Once you’ve finished shooting the paintballs, will find what you probably expected to see: a series of marks that have roughly the same shape and size as the slits themselves on the second wall. In other words, a splat that goes through one slit will hit the wall at a place that corresponds to the slit itself.
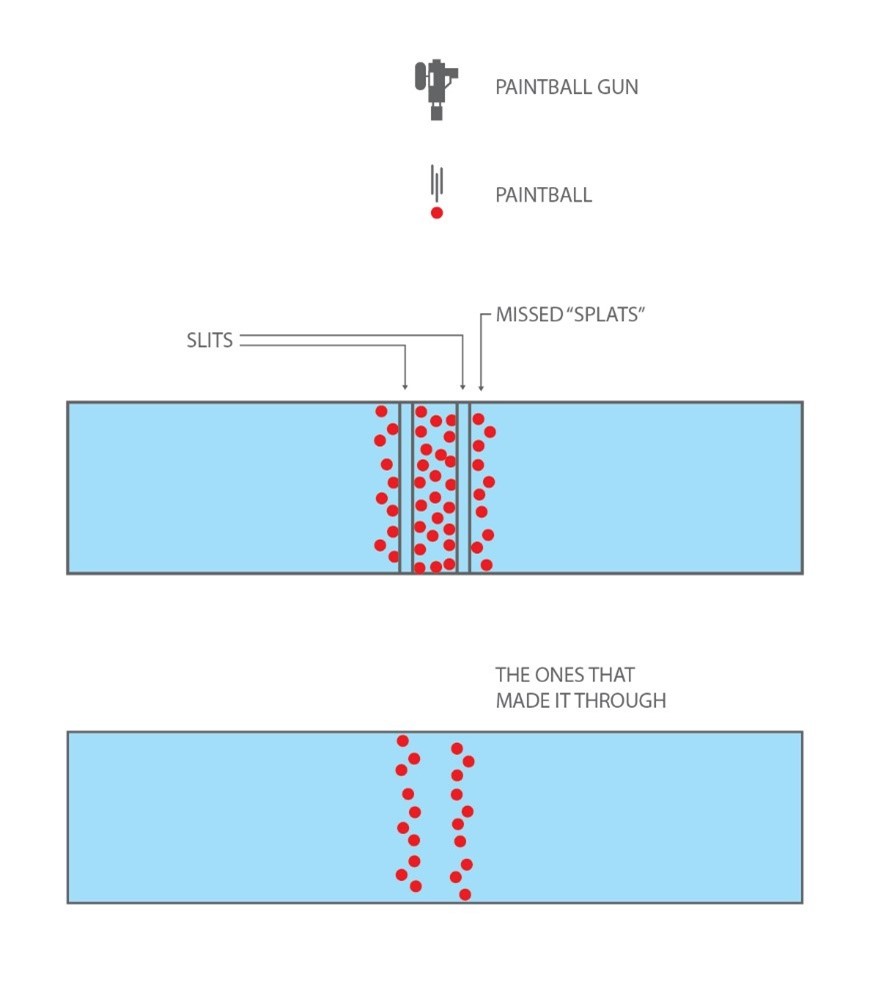
Now, if we perform the same experiment with photons instead of paintballs, the result is surprising. Take a light of a single colour and shine it towards the back wall through a wall that has slits. The pattern you will see on the back wall is not those discrete patterns we obtained with the paintballs; rather, we see what is called an “interference pattern” – the same kind of pattern we see when we push for example water waves through a slitted wall. The waves pass through both slits, splitting into two new waves. The crests of the waves and the troughs “interfere” with each other, meaning that when two crests meet, they reinforce each other, but when a crest meets a trough, they cancel out[4].
It appears then that the photons, which we thought were particles, also behave as waves. This is known as the “wave-particle duality” of quantum mechanics and means that what is colloquially referred to as particles (electrons, photons), somehow combine the characteristics of both waves and particles.
Uncertainty principle
Another key aspect of quantum mechanics is the uncertainty principle. In the classical world, we can measure both the position and the momentum of an object. In short, we can observe a car travelling on a highway, and with a fairly high degree of precision, measure both its position and its momentum. Measuring both quantities has no impact on the position and momentum of the car, and can lead to speeding tickets if one is not being observant of the speed limits on motorways.
In the quantum world, things are not so neat. The uncertainty principle states that the more precisely we know the position of a particle, the less precisely we have information about its momentum. In other words, before we make a measurement, we know nothing about the state of the system, but once we make a measurement, we collapse the system.
Superposition
It follows from the uncertainty principle that a quantum system remains in superposition, meaning that in a quantum system such as a photon, the photon can exist in a combination of multiple states corresponding to different possible outcomes. In other words, before we interact or measure the photon, it is in a state which corresponds to all states; when we interact or measure, the photon, it collapses into one of the possible definite states.
The superposition principle was famously illustrated by Edward Schrödinger, in his thought experiment about a cat in a box. In Schrödinger’s example, a cat is placed in a closed box. The box contains a vial of poisonous gas, which can be broken by a hammer. The hammer is connected to Geiger counter, which monitors a radioactive atom. The radioactive atom may or may not randomly decay, and if and when it does, the radiation will be picked up by the counter. The counter will then activate the hammer, breaking the vial of gas and killing the cat. The box being opaque (in the original thought experiment, it was a metal box), an observer of the closed system cannot “know” whether the cat is alive or dead. It is only when the observer opens the box (i.e., collapses the system), that the observer can determine whether the cat is in one or the other of the definite states. In the meantime, the cat is both alive and dead – it exists in a superposition of these two states.[5]
Entanglement
Another important feature of the quantum world is the notion of entanglement, of what Einstein referred to as « spooky action at a distance ».
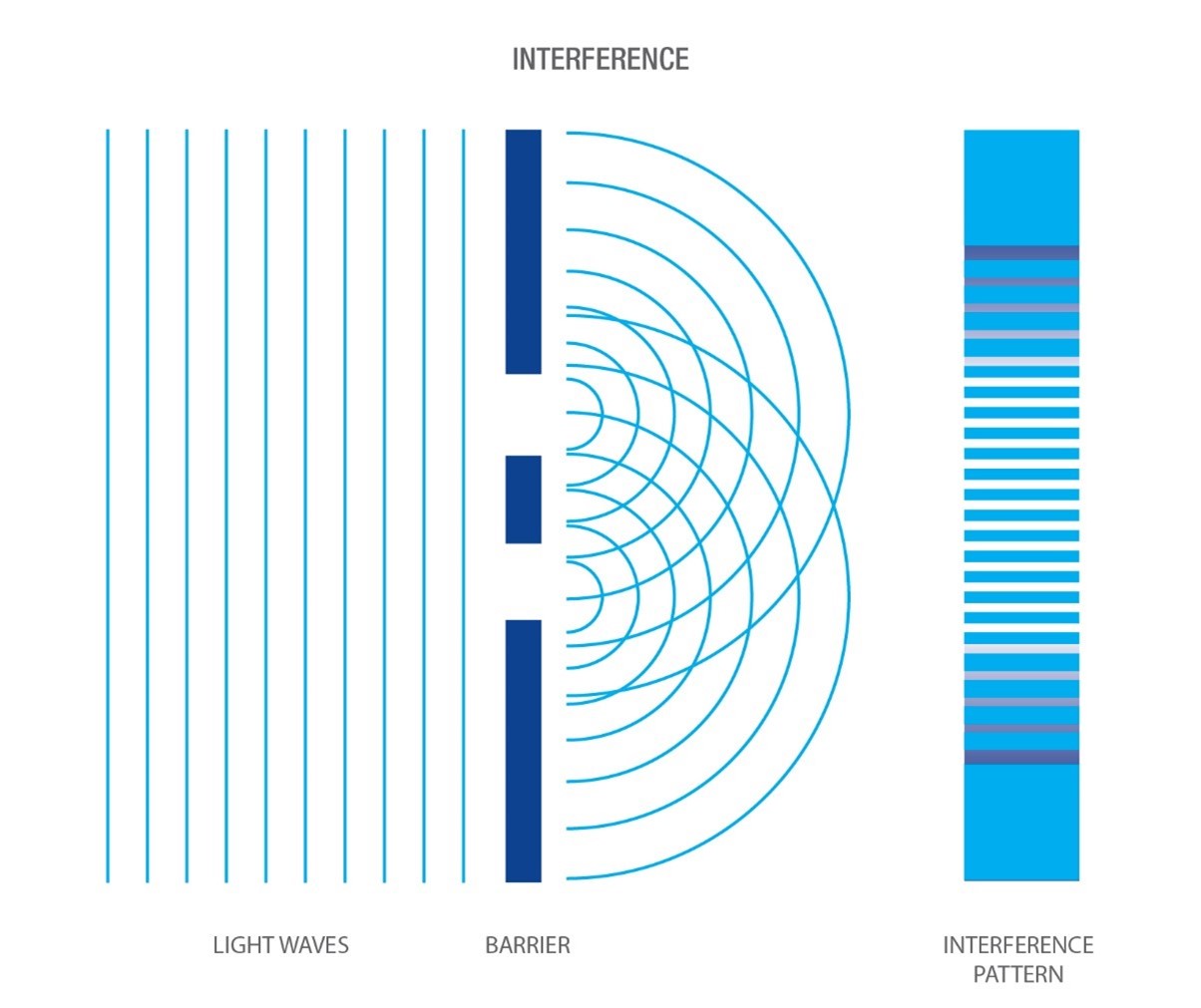
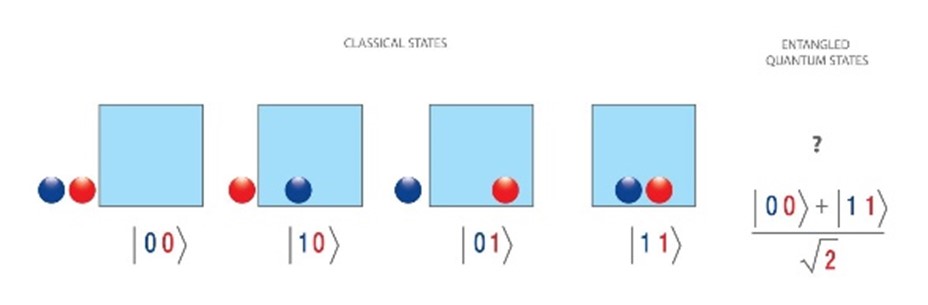
Applying the principle of superposition to a system composed of several objects, each of which can be found in several possible states, one can obtain very strange quantum states called entangled states. Take for example the illustrated example below. On the left, the system consists of a blue ball and a red ball each being able to be outside (0) or inside (1) a box. The superposed state in which the balls are simultaneously both outside and both inside the box is difficult to represent: it is at the same time very indeterminate (each of the balls can be found either inside or outside) but at the same time very determined because the balls are for sure at the same place.
Quantum algorithms[6]
A quantum computer is therefore a computing machine, which uses qubits instead of traditional bits. The qubits are the 1s and 0s of the classical computer; however, in order to fully take advantage of the qubits, a completely new way of approaching algorithms is needed: quantum algorithms.
Many books and articles have been written on quantum computing and quantum algorithms, the vast majority of which require advanced computer science or mathematics degrees to appreciate.[7] For the purposes of this article, I present the following, extremely simplified explanation.
The quantum algorithm uses quantum gates that act on the qubits to perform the calculations. Quantum algorithms allow the programmer to articulate the problem to be solved using quantum language, and thus inherently take advantage of the quantum features of entanglement and superposition.
One way to visualize a quantum algorithm acting on qubits is to represent the qubits by a series of balls arranged in a square array, floating in a liquid. The balls are all initially set into rotation in the same direction, and some balls are entangled, meaning that what happens to one ball also happens to the other entangled ball. Waves of varying amplitude and direction (the quantum algorithm) are directed towards the array of balls, which will cause some balls to change their rotation. Once the series of waves has terminated, observing the rotation of the balls yields the result to the calculation.
While this is helpful to visualize how a quantum algorithm interacts with qubits, there is a bit more to it than that.
The internal state of a quantum computer with N qubits is a vector of 2^N complex numbers. When a quantum gate operates on two qubits, it does the equivalent of applying a 2^N by 2^N rotation matrix to the vector representing the internal state, because each gate corresponds to a specific rotation matrix. Once the sequence of quantum gates is completed, one can then measure the qubits.
Measuring the qubits collapses the state of the quantum computer allowing an observer to “read” the result.
Quantum computers are inherently more powerful than classical computers for some problems because they're able to operate on 2^N numbers at once, given N qubits. They are also complicated because operations have to be expressed as a rotation matrix applied to the 2^N numbers.[8] The power of a quantum algorithm is its ability to articulate the rotation matrix required to obtain the desired result.
A common misconception regarding quantum computing is that because of the principle of superposition, all possible solutions to the problem are contained within the quantum computer and that the solution magically emerges when the system is collapsed. This is not the case. The qubits are acted upon using quantum principles, and a definite value is returned as the result of the calculations. In other words, although a quantum computer relies on quantum effects for its operation, the results of the calculations are deterministic.
Challenges Remain in Implementing Quantum Computers
While there have been significant advances in the realm of quantum science, and quantum computing, with at least a theoretical demonstration of quantum advantage, many challenges remain in implementing a quantum computer that provides a useful result. The third and final part of this series will examine the current state of development of quantum computing technologies.